【速算】 (a+b)(a-b)=a²-b²

(a+b)(a-b)=a²-b²のやり方

中学ぐらいのときになんかやったな～。
そうです。中学数学に登場する「因数分解」です。

私の中学の授業では、実際に数字を当てはめて便利に使おう！みたいなことはありませんでしたが、実はけっこう便利です。

早速、見てみましょう。

101×99

101×99
=(100+1)×(100-1)
=100²-1²
=9999

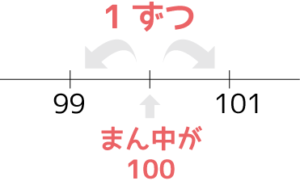
これはかなりわかりやすい例ですが、「まん中」がわかっちまえば楽勝です！

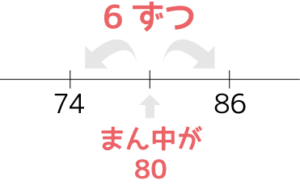
86×74

86×74
=(80+6)×(80-6)
=80²-6²
=6400-36
=6364

58×54

50に近い数の2乗がここで役に立ちます！

58×54
=(56+2)×(56-2)
=56²-2²
=3136-4
=3132

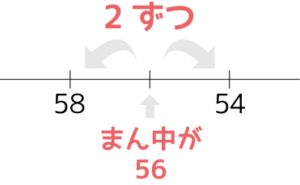
50台同士のかけ算、40台同士のかけ算はこれでもう神速です。
以下、いろいろなパターンを見てください。

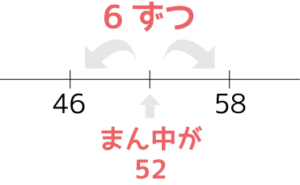
58×46

58×46
=(52+6)×(52-6)
=52²-6²
=2704-36
=2668

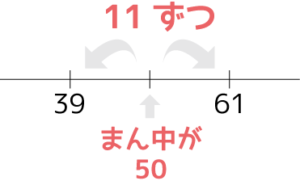
61×39

61×39
=(50+11)×(50-11)
=50²-11²
=2500-121
=2379

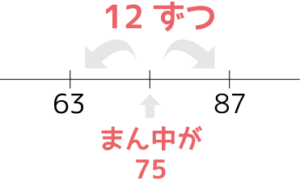
87×63

87×63
=(75+12)×(75-12)
=75²-12²
=5625-144
=5425+56（← 引き算を足し算に変換）
=5481

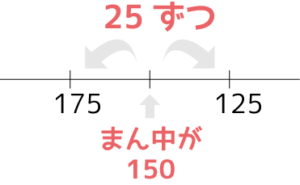
175×125

175×125
=(150+25)×(150-25)
=150²-25²
=22500-625
=22000-125
=21875

最大のポイントは、この公式が使えることに気がつくかどうかです。

ほかに使えるテクニックは……

主な速算のテクニックは以上になります。
調べればもっとたくさんのテクニックがありますが、実際に役に立つのはこんなもんだと思います。
あとは、「これ筆算やるのと手間はかわりないなぁ」ぐらいな感じです。

有名どころでは、因数分解で「(x+a)(x+b)=x²+(a+b)x+ab」というのがありますが、これを速算的に書き直すと、

(x+a)(x+b)=x(x+a+b)+ab

となり、たとえば「63×69」でやってみると

(60+3)(60+9)
=60×72+27
=4320+27
=4347

どうですか？私は好みではありませんｗｗｗ

私は「暗算」は別にできなくてもいいと思っています。
なにより「正確さ」が大事です。

最後にもうひとつだけ

これは、子どもたちには教えてません。
私が暇なときに考えて覚えたものです。
「2桁の2乗」

ただし、10の段、40の段、50の段、90の段、そして一の位が"5"のものはこれまでの速算法ですぐにわかるので、それら以外のものです。

これでさらに「(a+b)(a-b)=a²-b²」の応用範囲が広がるというわけですが、、、つづく




↓↓↓もっとおもしろいブログはこちら(*^_^*)

-かけ算, 小学校算数
-速算