逆さわり算（素因数分解、最大公約数、最小公倍数、約数の数）

「逆さわり算」って（勝手にそう呼んでる）、公倍数、公約数、最大公倍数、最大公約数、素因数分解とさまざまな場面で活躍するのに、中学以降ほぼ使わないですよね。
(逆さわり算ってこういうやつね↓)

だから大人はこれを見て「あぁ、こんなのあったな。」と何十年ぶりにその引き出しを開けるのです。

例題

24と36の公約数、最大公約数、最小公倍数を導いてみましょう。

公約数

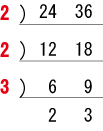
逆さわり算とはつまり素因数分解ですね。

24の約数は、「1, 2, 3, 4, 6, 8, 12, 24」
36の約数は、「1, 2, 3, 4, 6, 9, 12, 18, 36」
したがって24と36の公約数は、「1, 2, 3, 4, 6, 12」となります。

公約数を求めるときは、「2、2、3」のかけ算の組み合わせで成り立ちます。
2(を1個使う)=2
3(を1個使う)=3
2×2=4
2×3=6
2×2×3=12

約数の数

24を素因数分解すると、「2³×3」です。
したがって約数の数は、4×2=8個になります。

なぜこうなるのか？
これは場合の数(並べ方、選び方)で出てきます。中学か高校ぐらい？₅P₃とか₅C₃とか、あれです。

「2」を0個使った場合、1個使った場合、2個使った場合、3個使った場合の4通り。
「3」を0個使った場合、1個使った場合の2通り。
だから、4×2になるんですね。
指数に+1してかけるだけですが、これは0個の場合があるから+1しています。

36は「2²×3²」ですから、約数の数は3×3=9個です。

公約数は「2, 2, 3」の組み合わせですから、3×2=6個になります。

最大公約数

もう思い出されたかと思いますが、左側をすべてかけてやると最大公約数になります。
2×2×3=12
最大公約数は「12」です。

最小公倍数

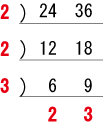
最小公倍数は、左側と下側の(分解された)数字をすべてかけてやります。
2³×3²=72
最小公倍数は「72」です。

素因数分解の早技（おまけ）

うちのチビたちは九九を覚えたときに、「逆さ九九」もやりましたので、すんなりでした。
解説抜きでご覧くださいwww

36 = 4×9 = 2²×3²
72 = 8×9 = 2³×3²
56 = 8×7 = 2³×7
120 = 12×10 = 3×4×2×5 = 2³×3×5




↓↓↓「ああ、思い出したわ！」と思ったらポチッとしてください

-小学校算数, 約数・倍数・素因数分解
-さかさ九九, 最大公約数, 最小公倍数, 約数, 素因数分解, 逆さわり算