階差数列の和【三角数】
長女のほうは小2の冬休みには中2数学までが完全に終わり、年が明けてから「なぞぺ~」「チャレペ~」とともに中学受験問題を題材にして家庭学習をしておりますが、その中に気になる問題がありました。
○を図のように正三角形の形に並べたときの○の総数1,3, 6, 10,…を三角数といいます。このとき,次の問いに答えなさい。
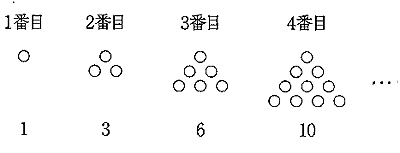
(1)50番目の三角数はいくつですか。
(2)1番目から7番目までの三角数の和はいくつですか。必要であれば,下の図を参考にして考えて下さい。
(3)1番目から30番目までの三角数の和はいくつですか。
三角数の一般項
1問目は「三角数の一般項」を求める簡単な問題。
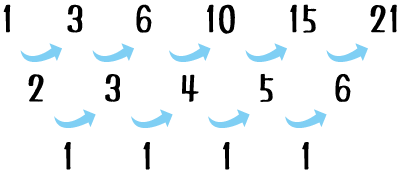
1番目は \(1\)
2番目は \(1+2\)
3番目は \(1+2+3\)
4番目は \(1+2+3+4\)
・・・・
50番目は \(1+2+3+……+50\) なので
\((1+50)\times50\div2=1275\)
「等差数列の和」を求められれば解ける問題です。
三角数の和
2問目、3問目はほぼ同じ問題ですが、「三角数の和」を求める問題です。
これ、小学生が解けるんかいな!?すげーな、中学受験生は!
とりあえず「三角数の和」をビジュアル化してみますた。月見団子だす。
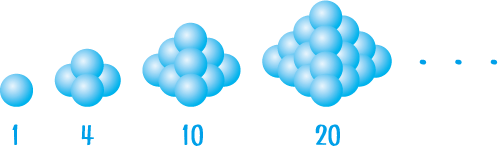
小学生でも理解できる解き方があるのか?
「階差数列の和」でググると高校数学の Σ を使った公式ばかりが出てきます。
まだこの問題中のヒントのほうがわかりやすい。
(2)
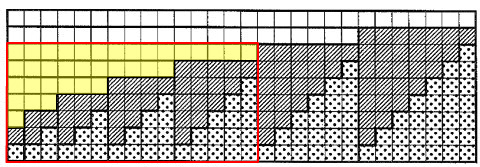
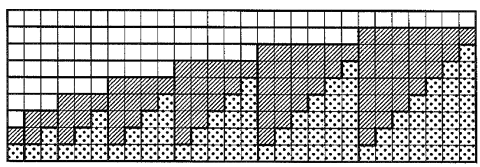
赤枠部分に注目すると、
求める点印部分と斜線部分、さらに黄色部分の個数が等しくなっていることがわかります。
つまり、求める個数は赤枠の \(\frac{ 1 }{ 3 }\) になります。
1番目から7番目までの長方形の
\(\begin{eqnarray}
ヨコ&=&1+2+……+7\\
&=&(1+7)\times7\div2\\
&=&28\end{eqnarray}\)
\(\begin{eqnarray}タテ&=&7+2\\
&=&9\end{eqnarray}\)
したがって、\(28\times9\div3=84\)
(3)
1番目から30番目までの長方形の
\(\begin{eqnarray}ヨコ&=&1+2+3+……+30\\
&=&(1+30)\times30\div2\\
&=&465\end{eqnarray}\)
\(\begin{eqnarray}タテ&=&30+2\\
&=&32\end{eqnarray}\)
したがって、\(465\times32\div3=4960\)
ちなみに、三角数の和を公式化すると、
\(\displaystyle S_n=\frac{ 1 }{ 6 } n ( n + 1 ) ( n + 2 )\)
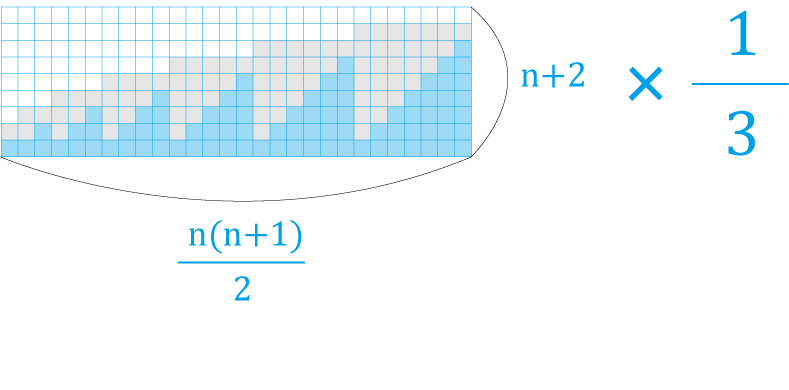
あれ?どっかで見たような……
\(\displaystyle \sum_{ k = 1 }^{ n } k^2 =\frac{ 1 }{ 6 } n ( n + 1 ) ( 2n + 1 )\)
\((=1^2 + 2^2 + \cdots + n^2)\)
ああ!平方数の和の公式とクリソツ。
平方数の和に関しても、先ほど三角数の和を導き出したやり方と同じようにできるのです。
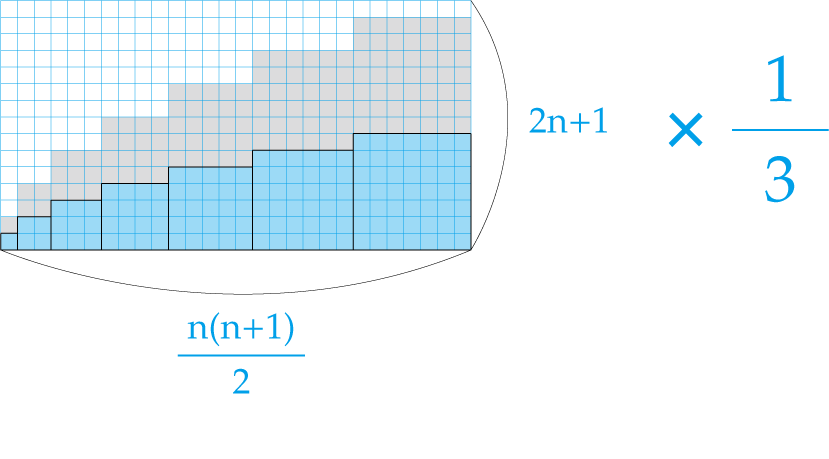
しかしこれ、小学生には難しすぎね?
↓↓↓「いいね!」の代わりにポチッとたのむ!