ジュニア算数オリンピック(2019)、図形問題の予想と結果
2019/06/16
予想
算数オリンピック・ジュニア算数オリンピックのトライアルの図形問題の予想です。
昨年はどんぴしゃで正十角形が出ました。
こういうのって、あまり予想とかしないほうがいいような気もしますが、所詮私ごときの勝手な予想なので、「まあいっか。」ということで。
早速予想ですが、近年よく出ている正多角形がやはり今年も出るんじゃないかと。
トライアルはやはり本戦に比べて易しめの問題が出されますから、「そんな補助線の引き方、思いつかねえよー!」みたいな問題は出ません。
分解していったら解ける程度の問題と予想します。
図形を重ねるとか、回転させるとかあるかもしれません。それを分解して解く。
あとは、あっても等積変形程度……かな。
つまり、正六角形・正八角形・正十角形の分解と等積変形を押さえておけばOK?!
この記事は後日、試験終了後に続編を書きたいと思います。
結果
正多角形の分解というところまでは当たってましたね^^;
ジュニア算数オリンピック トライアル 問題5
図は、面積が72㎝2の正十二角形に、正十二角形と1辺の長さが等しい正三角形を組み合わせた図形です。色のついた部分の面積は何㎝2ですか。
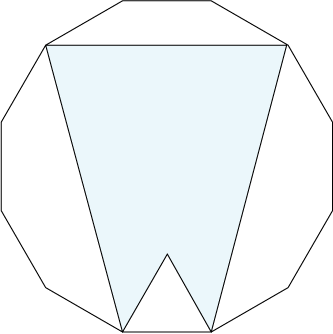
図は、面積が72㎝2の正十二角形に、正十二角形と1辺の長さが等しい正三角形を組み合わせた図形です。色のついた部分の面積は何㎝2ですか。

説明はいらないと思いますが、、、
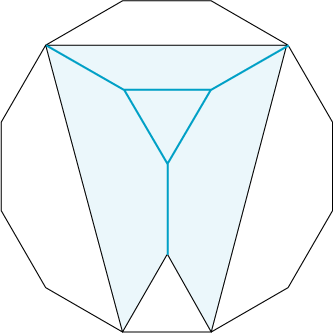
36㎝2ですね。
ジュニア算数オリンピック トライアル 問題9
下の図のように、直角三角形が2つあります。アとイの角の和を求めなさい。
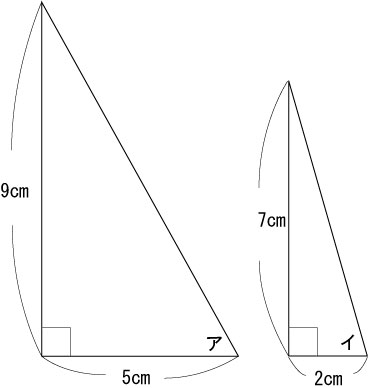
下の図のように、直角三角形が2つあります。アとイの角の和を求めなさい。

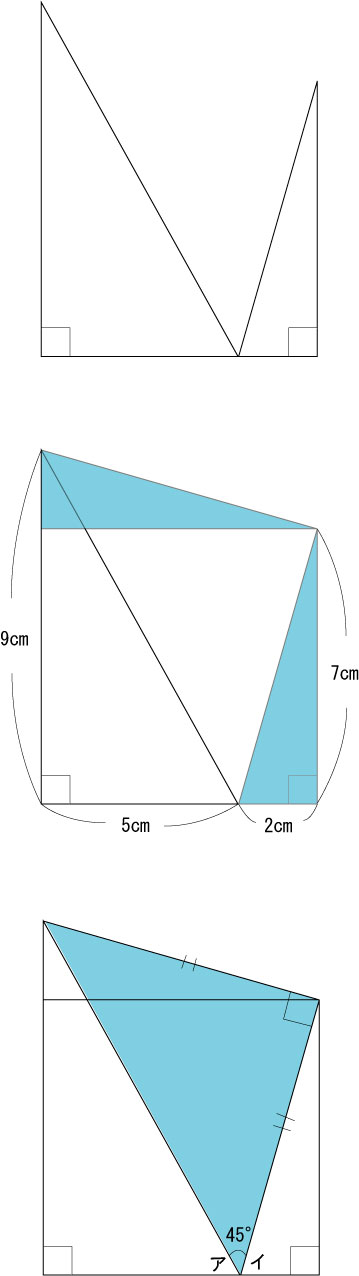
ア+イ=135°