チェバの定理とメネラウスの定理をてんびん算と連比で解く
2017/09/06
チェバ・メラをてんびん算で攻略
辺でも中線でも、どれか2つの比がわかっていれば、すべての比がわかります。
例題)
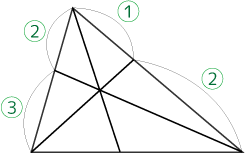
まずはひとつの辺に注目し天秤に見立てる
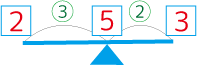
アルキメデスのテコの原理
左側に2kgのおもりを載せたら、右側には3hgのおもりを載せるとこのシーソーが釣り合います。
まん中の支点部分には総重量の5kgの重さがかかっています。
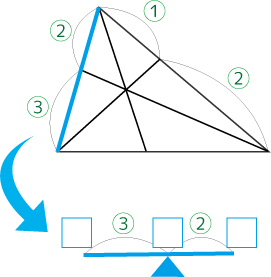
連比
ひとつの頂点に、3つの天秤がかかっています。
実際気にするのはふたつでよいのですが、ふたつの天秤が同時に成り立つようにおもりの重さを決めていきます。
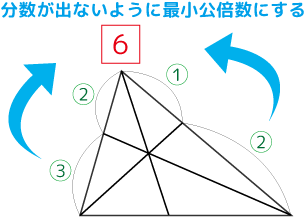
一方のおもりの重さがわかれば、もう一方のおもりの重さもわかる
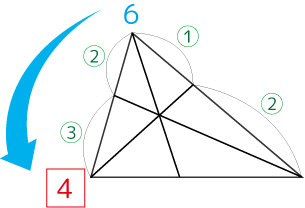
両端の重さが決まれば総重量もわかる
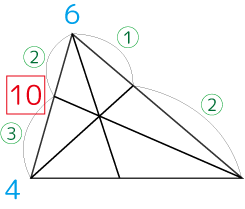
右側の辺も同様
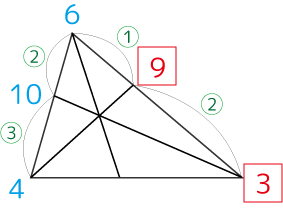
底辺の総重量もわかりました
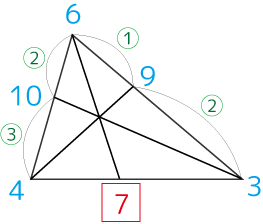
底辺の比がわかりました
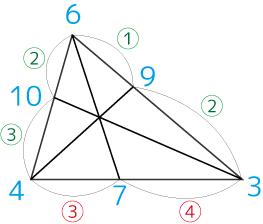
中線の比もすべてわかりました
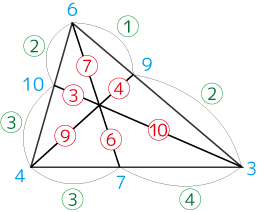
「交点は重心になっている」ってなんで教科書に書かない?
すべての辺と中線においててんびんが釣り合った状態であるのだから、その三角形のバランスの中心であることがわかります。
素材が均一にできている三角形の板があればその重心は、辺の中点と頂点を結んでできる中線の交点になる。というのは数学的な重心です。
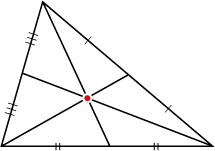
もし、素材が不均一にできていたり、おもりをぶら下げてみたときには、その三角形の板の重心(質量中心)はチェバの定理が成り立つ交点となります。
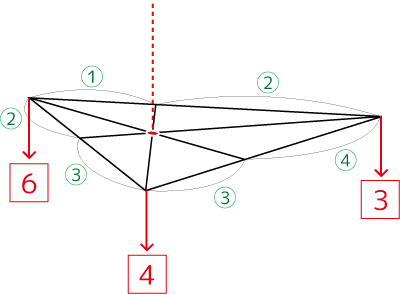
三者のパワーバランスモデル
幾何学的、物理学的な応用はもちろんのこと、例えばあらゆる三者のパワーバランスの表現に用いてもよいのではないかと。
経済学、料理、組織、身体能力……
なんにでも使えるのではないでしょうか?
例えば、「親」の権力が強い学校があったとします。このままでは学校の運営に支障があるので「先生」が奮闘します。
チェバ式でいくなら問題解決のために「親vs先生」という構図だけではなく、「生徒」(生徒会)による学校運営の比重も増やすことで、全体のバランスが取りやすくなる。
あるいは、「先生」と「生徒」の距離をつめることで「親」の相対的重量を軽くする。ということができます。
↓↓↓ 励みにポチッとお願いします