【過不足算(差集め算)】基礎から入試問題まで
「そういえば、息子のほうにはまだ過不足算を教えてなかったな」
ということに気づき、夏休みを利用して教えることに。お姉ちゃんの復習がてら。
過不足算は線分図で解くやり方と、面積図で解くやり方の2通りありますが、面積図のほうが簡単で理解しやすいため、基本的には面積図の解き方がオススメ。
基礎編
まず、それぞれの面積図を描きます。
いきなり重ねた図を描かないで、一度それぞれの図を描いてから、「どう重ねようか」考えた方がいいと思います。
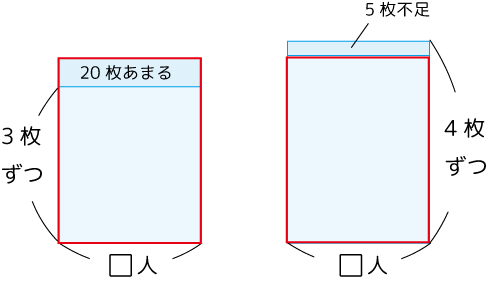
赤枠はもともとの折り紙の枚数です。
ここがポイントで、もともとの数はどの部分が表しているのか、確認を入れます。
この確認を入れないとミスの元になります。
第一に、「余る」とか「足りない」という言葉に惑わされて、面積図を書き間違えてしまうことがあります。
「□人に3枚ずつ配るときに必要な枚数」+20枚が、もともとの折り紙の枚数です。
一方、「□人に4枚ずつ配るときに必要な枚数」は、もともとの枚数+5枚です。
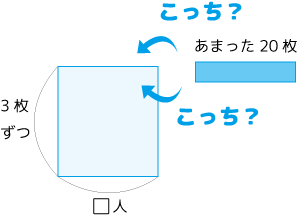
また、2つの図を重ねるときに、どの部分とどの部分が同じなのかも注意ポイントです。
もともとの数(赤枠)の確認をしてあれば、ミスなく楽々重ねられます。
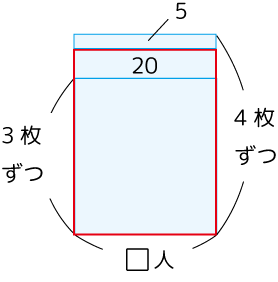
で、ここから先は下図のようになりますが、説明省略。
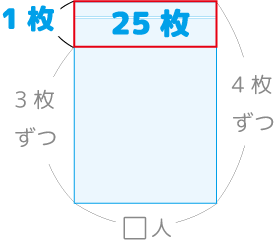
答:25人、95枚
説明省略。
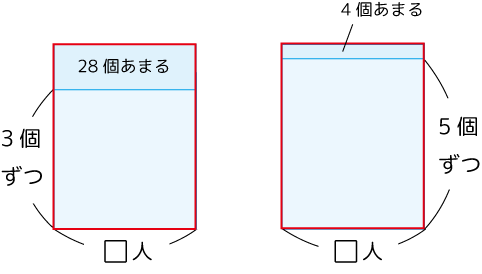
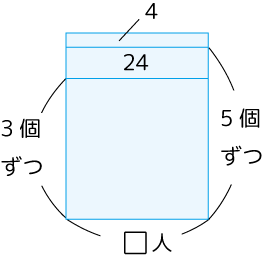
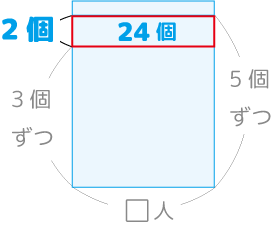
答:12人、64個
説明省略。
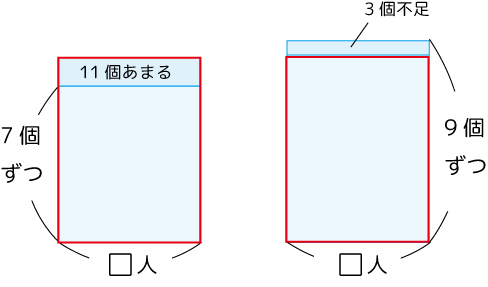
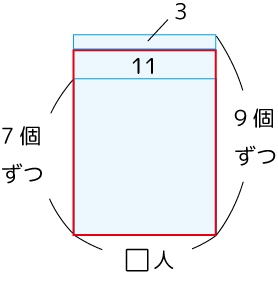
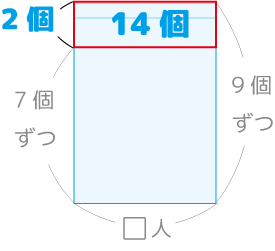
答:7人、60個
入試問題
まず、問題の通りに図を描いてみます。赤枠はもともとのカードの数。
いきなり図形を重ねない方がいいと言いましたが、入試問題レベルになると、よりそう感じますね。
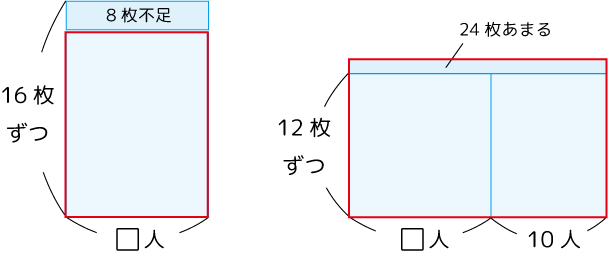
右側の図を整理します。
後から加わった10人には、120枚配ったことが分かります。
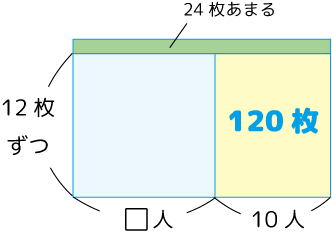
これを変形します。
□人に12枚ずつ配ると、144枚余ることが分かります。
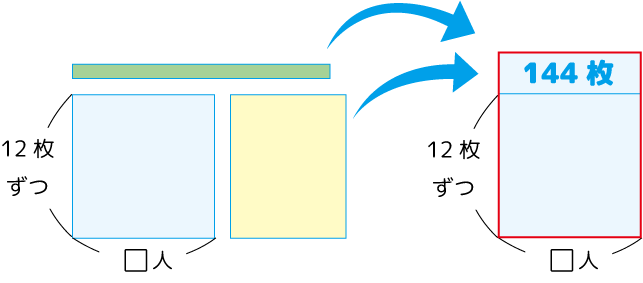
ここまで来たら、基礎編とまったく同じ。
もう一度、図形を並べます。
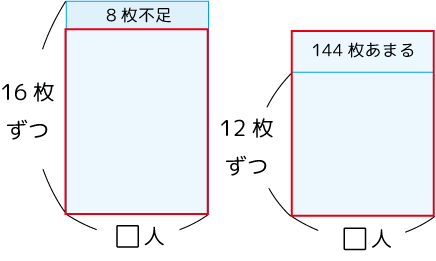
図形を重ねます。

できあがり。
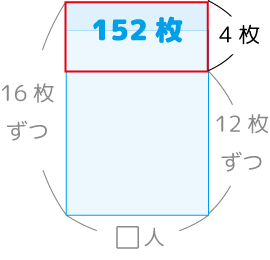
答:38人、600枚
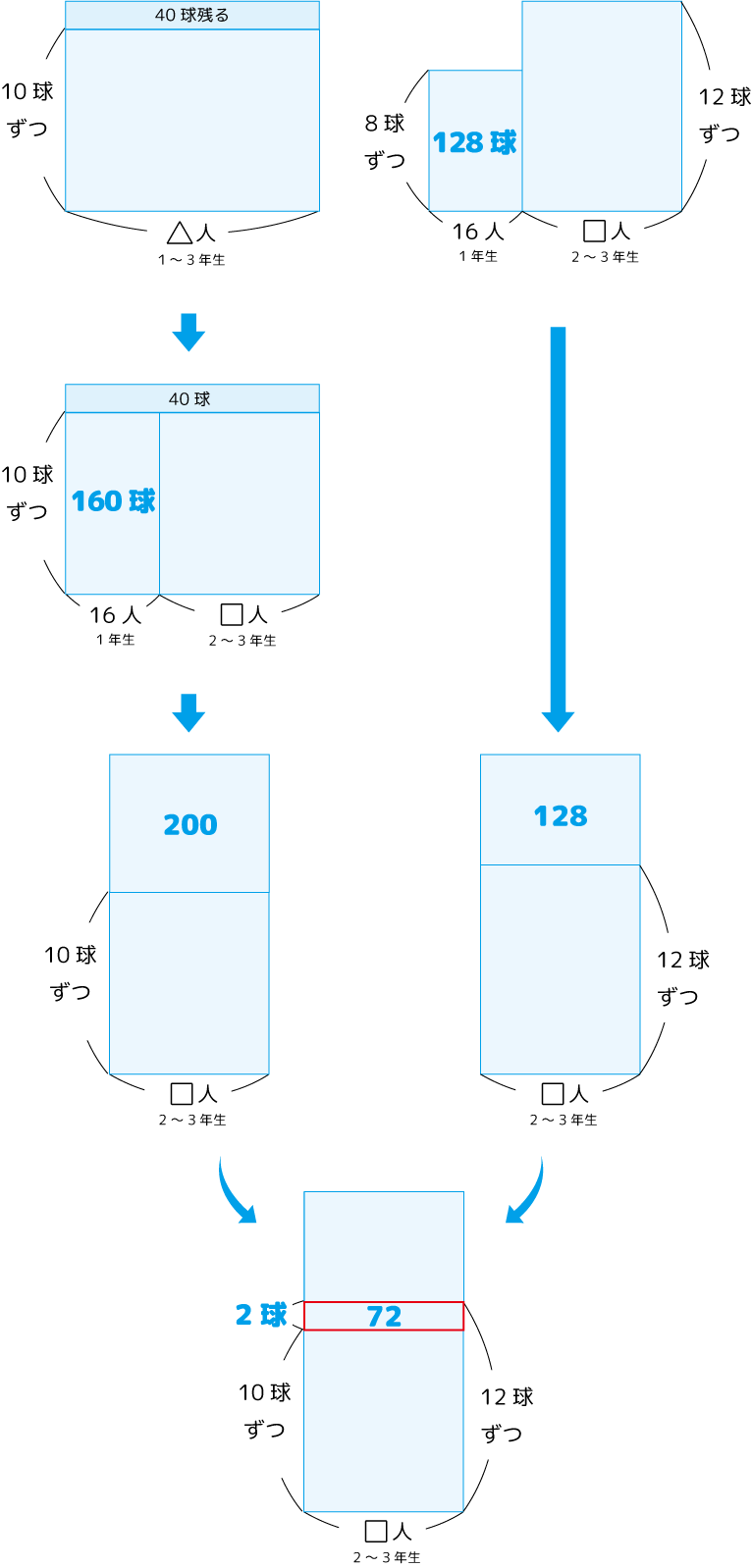
答:560球(2~3年生は36人、全生徒で52人)
問題文をそのまま図に表します。
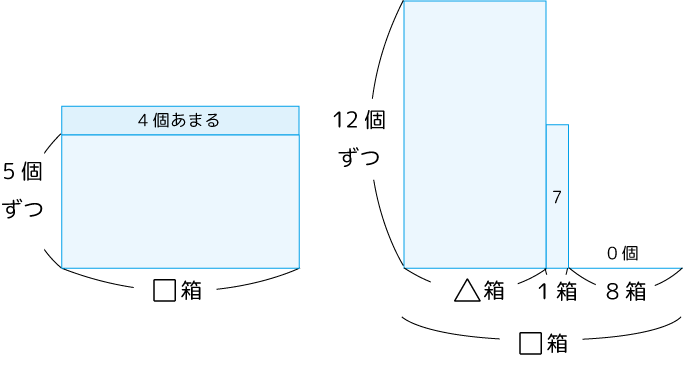
右図の空き部分が何個分なのか。
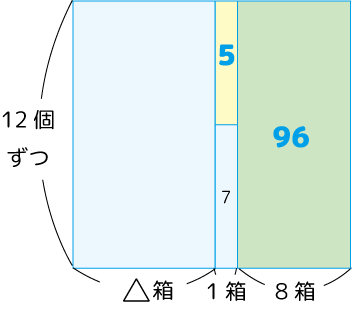
つまり、□箱に12個ずつ入れようとすると、101個分の空きができるということ(右図)。
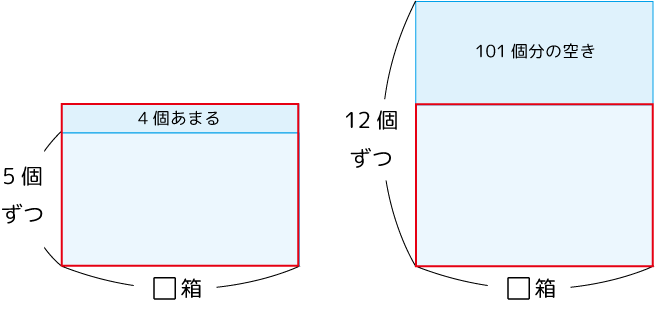
あとは基本通り。
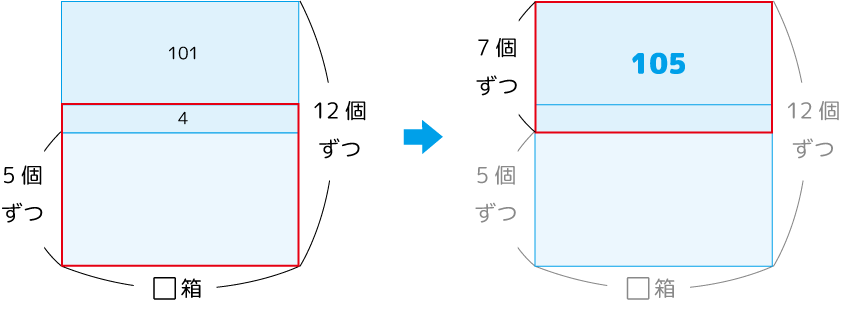
答:79個(箱は15箱)
特殊算はだいたい2次方程式で解けちゃうんですけどね。
過不足算も2次方程式ができると一発で解けてしまいます。
でもまあ、頭の体操的な意味で、図形を使って解いてみよう!てな感じです。
↓↓↓「いいね!」の代わりにポチッとたのむ!