【図形】正五角形の分解
正五角形の性質
正三角形・正方形・正六角形に引き続き、正五角形編です。
相似
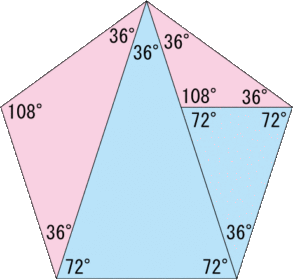
まずは角度に注目。
内角の和が540°なので、1つの内角が108°。
対角線を引いたら内角が3等分されます。
分解してできる三角形の内角は、36°、72°、108°の3種類。
そして、36°:72°:108°=1:2:3 になっています。
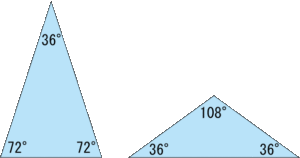
大体、どこをどう切り取ってもこの2種類の三角形が出来上がります。
相似の三角形がたくさんできるということ。
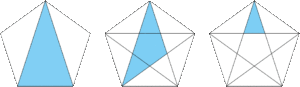
等脚台形
辺と対角線が平行になっているのがポイントですね。
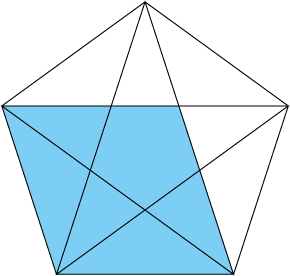
したがって、2つの青く塗った三角形も相似です。
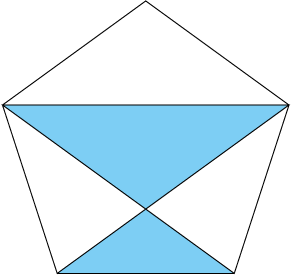
菱形
菱形も隠れてますね。
平行四辺形な上に、辺の長さが等しいので菱形というわけですね。
正五角形の部品で正十角形ができる
とんがり帽子型の三角形の尖った部分が36°なので、十角形ができます。
そう思うと、36°って数字が記憶に残りやすいですね。

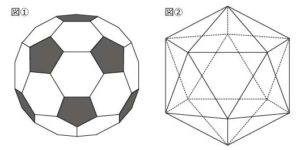
サッカーボール
サッカーボールは三十二面体。
三十二面体は正二十面体からから作れます。
正五角形12個、正六角形20個。
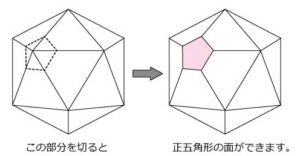
正二十面体の頂点は12個だから、切り落とした部分の正五角形は12個できます。
残った正六角形はもとの面の数と同じ20個になります。
頂点は正五角形のまわりに必ずあるから、5×12=60個と計算すれば求められます。(頂点の数=60)
正五角形は12個なので辺の数は「12×5=60」、正六角形は20個で「20×6=120」。
1つの辺に正五角形と正六角形がくっついているから、足した数字を2で割ると90。(辺の数=90)
正多面体は5種類しかない

オイラーの多面体定理:
頂点の数 - 辺の数 + 面の数 = 2
| 面の形 | 面の数 | 辺の数 | 頂点の数 | |
| 正四面体 | 正三角形 | 4 | 6 | 4 |
| 正六面体 | 正方形 | 6 | 12 | 8 |
| 正八面体 | 正三角形 | 8 | 12 | 6 |
| 正十二面体 | 正五角形 | 12 | 30 | 20 |
| 正二十面体 | 正三角形 | 20 | 30 | 12 |
算数オリンピック2016年 jr.トライアル
【問題】正十角形の色のついた部分の面積が100cm2のとき,この正十角形の面積は何cm2ですか。
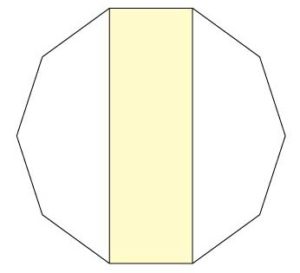
補助線として黄色の四角形の対角線を引きます。
すると、面積の等しい4つの三角形に分かれます。
1つ分は100÷4=25cm2
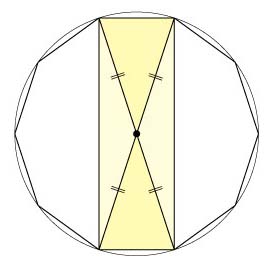
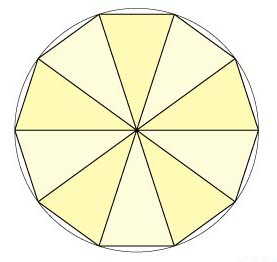
25cm2の三角形が10個あるので、25×10=250cm2
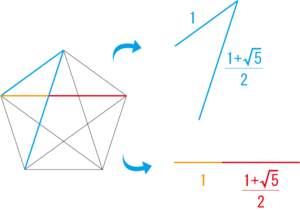
黄金比(おまけ)
一辺と対角線の比は「黄金比」となっており、
(=1.618)
また、対角線はほかの対角線によって黄金比に分割されます。
先ほどの2種類の三角形の辺の比も黄金比となっています。
対角線を全部引いたら星型ができあがり、中に小さな正五角形が現れます。
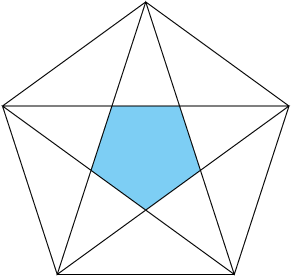
大きい正五角形と小さい正五角形の辺の比は、
面積の比は、
大:小=2:7-3√5
(計算、証明は割愛)
平方根がバンバン出てくるので、小学生には無用かも知れませんが、π=3.14 が許されるなら、61.8% と 38.2% は雑学的に知ってても悪くないと。株をやる人はよくご存じのフィボナッチですね。
おまけに折り紙で正五角形を作って見ましょう!
↓↓↓「正五角形に対角線を引くと検尿の紙コップを思い出すわっ!」という人はポチッとしてください