ならしてそろえる平均算

平均の考え方

１．「足して割るのが平均」
２．「ならしてそろえるのが平均」

中学に入って \(x,y\) を使った式を習ってしまうと、便利が故に図形のイメージはせず、数式のパズルを解くだけになってしまいがち。やはり図形的なイメージは持っておきたいところ。

わかっちゃえば簡単だけど、理解するのにスンナリではないかも。

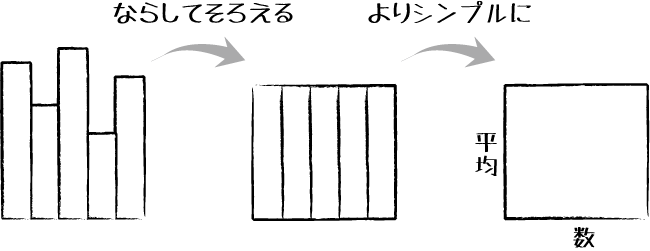
問題１

オーソドックスな出っぱり変形問題です。この問題は、合計して5で割ってもできますけどね。問題パターンによってはこのやり方は知っておくべき。

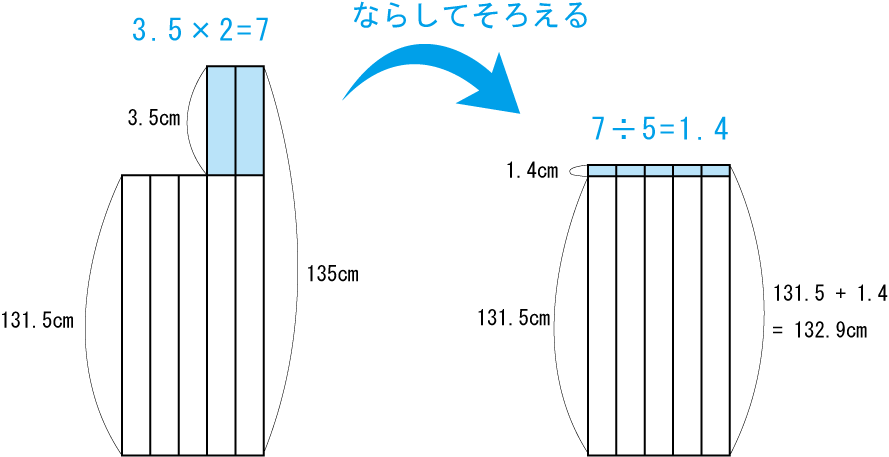
（答）132.9cm

問題２

今度は変形技を使わないと解けません。

(1) クラス全体

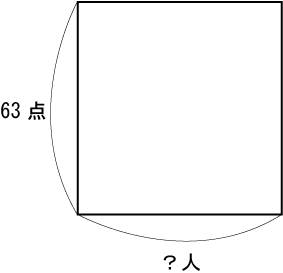
(2) Ａくんの出っぱりを変形（全員に均等に分配）

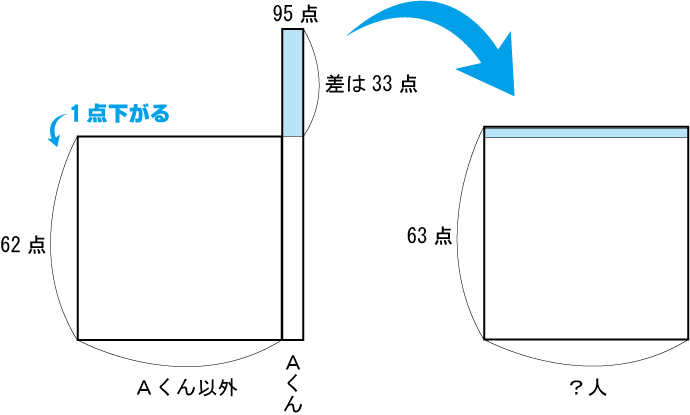
(3) もちろん同じ33点

(4) 答えは一目瞭然

（答）33人

ちなみにｘを使って解いてみると

\(63x=62(x-1)+95\)
\(63x=62x+33\)
\(x=33\)

問題３

面積=合計 というチョー簡単問題。

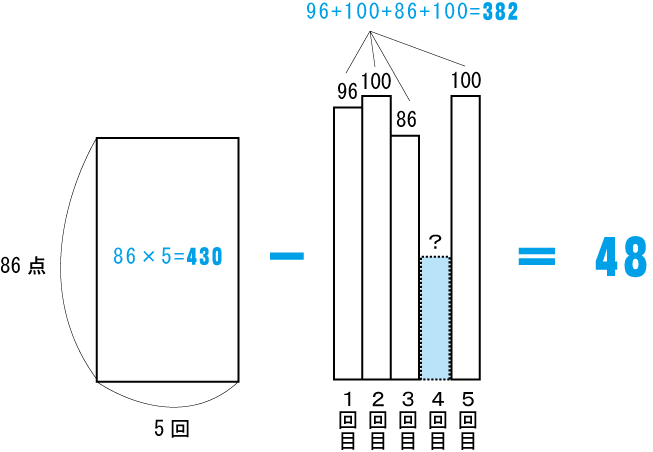
（答）48点

問題４

出っぱり変形のちょいムズ問題です。この問題、xを使うと途端に簡単になるんですけどね。

(1) クラス全体の合計点と、男子と女子の合計点の和は当然同じ。

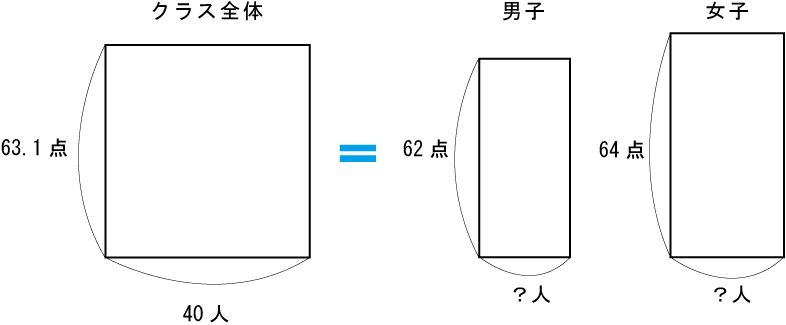
(2) 出っぱりをならす。高さはクラスの平均点に合わせる。

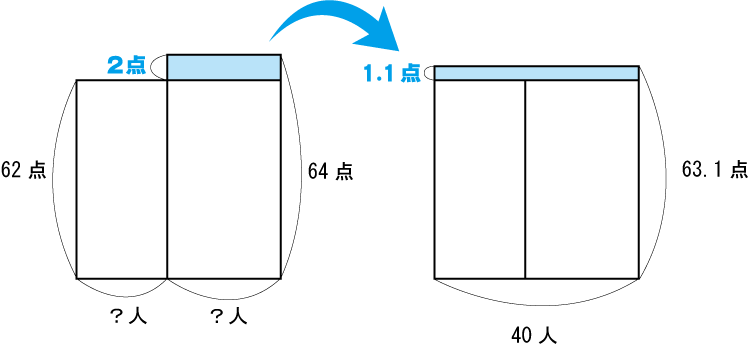
(3) これがスンナリ理解できるかな？というところ。

（答）22人

ちなみにｘを使って解いてみると

\(63.1\times40=62(40-x)+64x\)
\(2524=2480-62x+64x\)
\(2x=44\)
\(x=22\)

問題５

「問題2」とまったく同じ解き方。

(1)

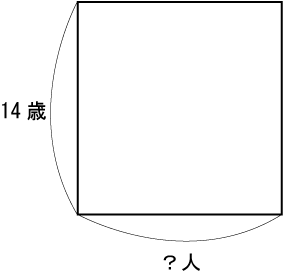
(2)

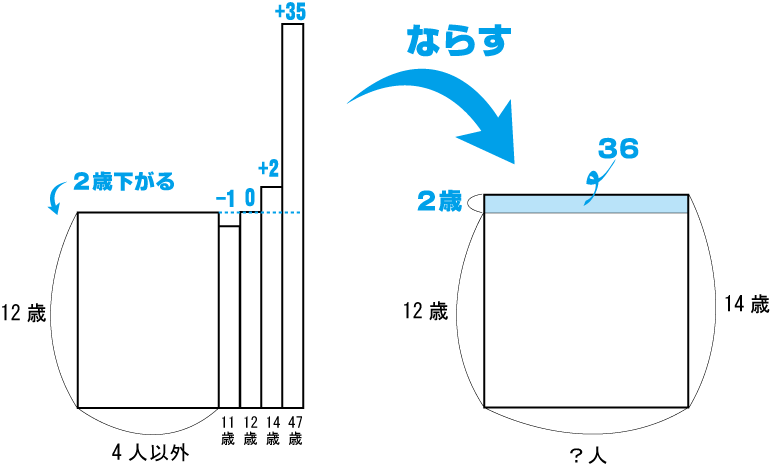
（答）18人

ちなみにｘを使って解いてみると

\(14x=12(x-4)+(11+12+14+47)\)
\(14x=12x-48+84\)
\(2x=36\)
\(x=18\)




↓↓↓「\(x\) 使ったほうが簡単に見えるわっ！」と思った人はポチッとしてください

-小学校算数, 平均