小学校算数 場合の数 算数オリンピック・世界算数・MASSE
【場合の数】2013年ジュニア算数オリンピック
2019/01/21
問題
図の9つの正三角形のマスに次の規則に従って、1~9の数字を1個ずつ入れていきます。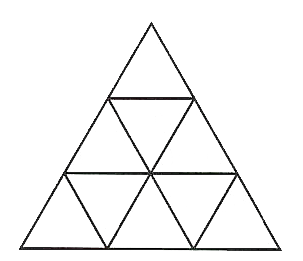
図の9つの正三角形のマスに次の規則に従って、1~9の数字を1個ずつ入れていきます。

規則:辺で接している2つの正三角形に入れる数字は、左側にあるもの、上側にあるものに大きな数字を入れる。
たとえば、次の例のように入れると規則を満たしています。
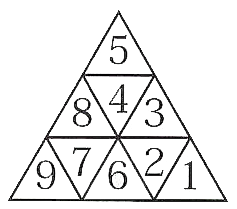
このとき、規則を満たす数字の入れ方は、例の場合をふくめて全部で何通りありますか。
正答率が1.2%の問題です。
下↓↓に解説が書いてありますが、答えを見る前にお父さんお母さんにチャレンジしてみてほしい。
これどうやって解き始めたらいいかわかりますか?
これを小学4~5年生が解くんですからねえ。しかも、これでまだトライアル。
まずは、本に載っていた解説がこちら↓↓
正答率1.2%
まず、1と2に関しては、記入する場所が1通りに決まります。次に、3の入る場所を考えます。3は2の上か、左側に入りますが、これは、1と2を記入した三角形を中心に折り返すことで重なります。よって、上側の場合を数えて2倍すればよいです。
次に、3の左側に入れる数が何かを考えます。
■4の場合
4の上側に入れる数は、5~9のいずれでもよいので5通り。そして、残った4つの数2×2の正三角形に規則に従って入れればよいです。これは、小さい数2つの入れ方が1通りに決まりますので、残りの2つをどちらに入れるかで2通りあります。
よって、5×2=10通りです。
■4以外の場合
5,6を入れた場合は、先ほどと同様に考えることができて、上側に入れられる数字が4通り、3通りですので、(4+3)×2=14通りです。
次に、7を入れた場合を考えます。7の上側と左側には必ず8と9が入ります。よって、どちらに8を入れるかで2通りあります。残りの3つの数は横に並んだ3つに入れますので1通りの入れ方しかありません。よって、2×1=2通りです。
8以上を入れてしまうと、上か左側が必ず8より小さい数になってしまいます。
以上より、(10+14+2)×2=52通り。答え:52通り
まず、1と2に関しては、記入する場所が1通りに決まります。次に、3の入る場所を考えます。3は2の上か、左側に入りますが、これは、1と2を記入した三角形を中心に折り返すことで重なります。よって、上側の場合を数えて2倍すればよいです。
次に、3の左側に入れる数が何かを考えます。
■4の場合
4の上側に入れる数は、5~9のいずれでもよいので5通り。そして、残った4つの数2×2の正三角形に規則に従って入れればよいです。これは、小さい数2つの入れ方が1通りに決まりますので、残りの2つをどちらに入れるかで2通りあります。
よって、5×2=10通りです。
■4以外の場合
5,6を入れた場合は、先ほどと同様に考えることができて、上側に入れられる数字が4通り、3通りですので、(4+3)×2=14通りです。
次に、7を入れた場合を考えます。7の上側と左側には必ず8と9が入ります。よって、どちらに8を入れるかで2通りあります。残りの3つの数は横に並んだ3つに入れますので1通りの入れ方しかありません。よって、2×1=2通りです。
8以上を入れてしまうと、上か左側が必ず8より小さい数になってしまいます。
以上より、(10+14+2)×2=52通り。答え:52通り
わかりにくいですが、やり方としてはこの通りですね。
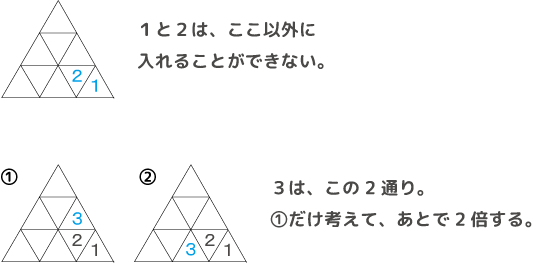
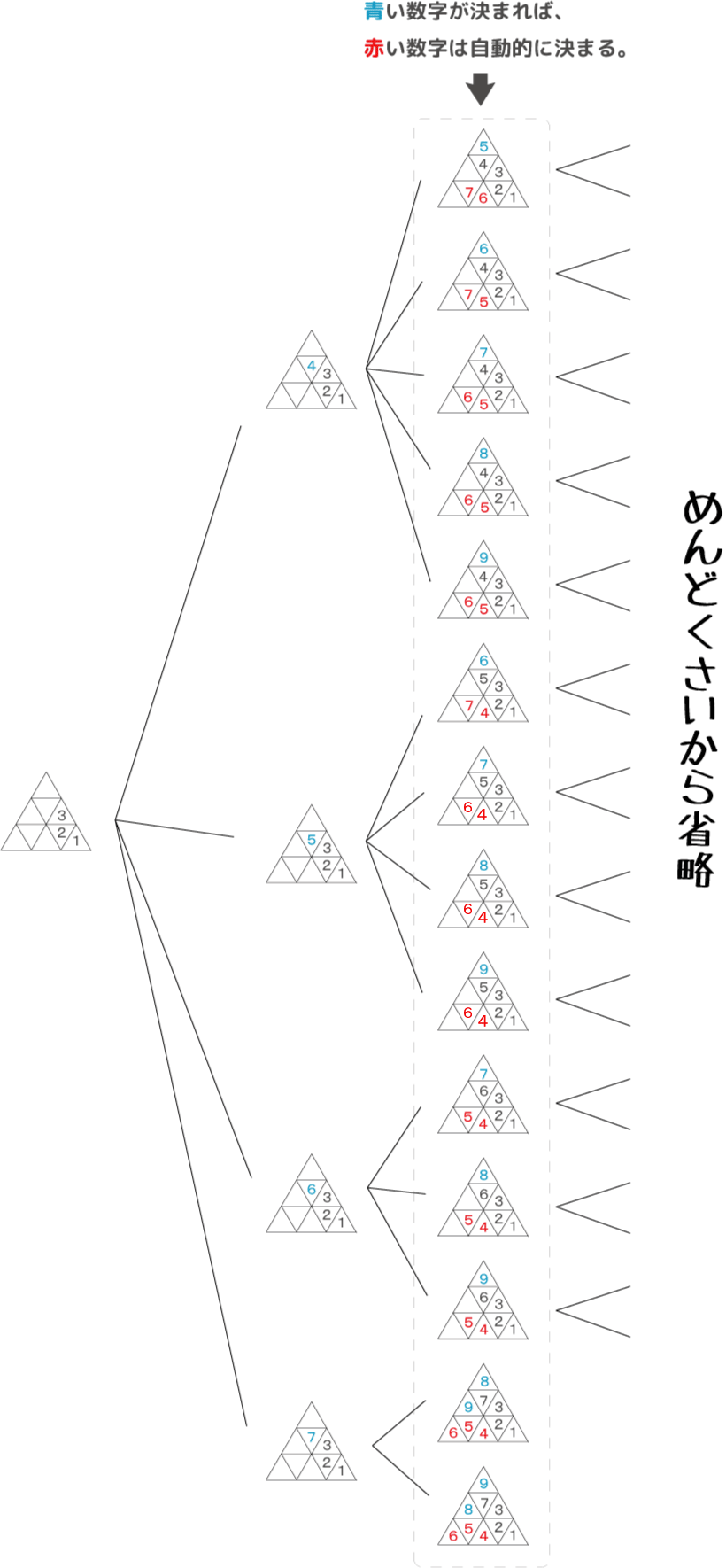
3が2の左側にあるときも同様なので26通り×2で52通り。
↓↓↓「いいね!」の代わりにポチッとたのむ!