算数オリンピックにありそうな問題（中学受験問題から）【条件整理】

2017/02/10

今年の算数オリンピックに参戦する方向で検討中です（長女）。
練習にと思って「なぞぺ～」「ちゃれぺ～」もちょいちょい取り組んでいますが、中学受験問題の中にちょうどこの分野の問題があるのを見つけました。「そんなの常識」なのかもしれませんが、なにしろ私は中受未経験です。

ひとまず先に、私が試しに解いてみました……
まあ簡単に解けたのですが、これ算数の知識はいらないし、論理的に考えられれば解けちゃう問題なので、実際の受験の時は得点を稼ぐところなんでしょうか？
算数オリンピックで言えばキッズBEE（小1～小3）レベルかなと思いますが。

さて、長女にもやらせてみました。

３位と５位はだれ？（2016年　東洋英和女学院中学部）

運動会の徒競走で、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆの６人が同じ組で走りました。
６人は、結果について次のように言っています。
Ａ「Ｆは私より先にゴールしました。」
Ｂ「Ａに勝つことができました。」
Ｃ「Ｆは３位までに入ることができませんでした。」
Ｄ「Ｃに勝てると思っていたのに、残念でした。」
Ｅ「Ｄには最後まで追いつけませんでした。」
Ｆ「Ｂにはー度ぬかれましたが、ぬき返しそのままゴールしました。」
３位の人と５位の人はだれですか。

○ 正解
それぞれの発言をそのまま書き出してみると、自ずと答えが出てくる簡単問題。

1位：Ｃ
2位：Ｄ
3位：Ｅ
4位：Ｆ
5位：Ｂ
6位：Ａ

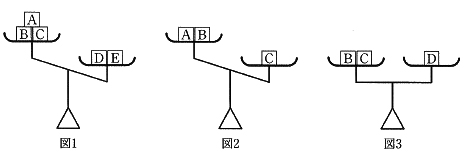
Ａ、Ｂ、Ｃ、Ｄ、Ｅのおもりは何ｇ？（2016年　大妻多摩中学）

Ａ、Ｂ、Ｃ、Ｄ、Ｅのおもりがあります。
重さは１ｇ、２ｇ、３ｇ、４ｇ、５ｇのどれかで、同じ重さのおもりはありません。
これらのおもりをてんびんにのせると図１〜３のようになりました。
(図３は、ちょうどつりあっています)
Ａ、Ｂ、Ｃ、Ｄ、Ｅのおもりはそれぞれ何ｇですか。
bandicam_20160315_074057922

○ 正解
長女はなぜかおもり問題が大の得意です。

Ａ：2g
Ｂ：1g
Ｃ：4g
Ｄ：5g
Ｅ：3g

２ｇの玉と３ｇの玉は？（2016年　ラ・サール中学）

６個の玉、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆのうち、４個が１ｇ、１個が２ｇ、1個が３ｇです。
Ｂ、Ｃ、Ｄの重さの和と、Ｅ、Ｆの重さの和が等しく、
Ａ、Ｃ、Ｄ、Ｅの重さの和よリもＢ、Ｆの重さの和が大きいとしたら、
２ｇの玉と３ｇの玉はＡ～Ｆのうちどれですか？

○ 正解
同じく得意なおもり問題。

Ｂ：2g
Ｆ：3g

優勝した合計得点は？（2016年　海陽中等教育学校）

ある年の運動会で赤組、青組、黄組、緑組から２名ずつの８人が１５００ｍ走に出場しました。
得点は１位１００点、２位９０点、３位８０点・・・８位３０点のように１０点きざみで、このレースで同着はありませんでした。
次の３人の証言から黄組の合計得点として考えられる点数を答えなさい。
Ａ：黄組と赤組の合計得点は等しく同点で優勝しました。
Ｂ：緑組と黄組の合計得点の差は２０点でした。
Ｃ：２位となった選手は黄組でした。

○ 正解
条件に合うように試していくだけですね。

黄組：150点（90点、60点）
赤組：150点（80点、70点）
緑組：130点（100点、30点）
青組：90点（50点、40点）

思い浮かべた数はいくつ？（浦和明の星女子中学　2013年）

Ａさんに０から６３までの数のうち１つを重い浮かべてもらい、
その数についで６つの質問をしたところ、答えは次のようになりました。
Ａさんの思い浮かべた数はいくつでしょうか？
(ア)その数を２で割りた余りは１ですか。「はい」
(イ)その数を４で割った余りは２以上ですか。「はい」
(ウ)その数を８で割った余りは４以上ですか。「いいえ」
(エ)その数を16で割った余りは８以上ですか。「はい」
(オ)その数を32で割った余りは16以上ですか。「いいえ」
(カ)その数は、32以上ですか。「はい」

× 不正解
この問題はできなそうだなと思ったらやっぱりできませんでした。どの問題もそうですが、問題文に圧倒されて解くきっかけがパッと見わからないと、もうダメですね。落ち着いて一個一個見ていったら大したことないんですけどね。

(ア)と(カ)より、３３～６３までの奇数、
(オ)より、３３～４７までの奇数、
(エ)より、４１、４３、４５、４７
(ウ)より、４１か４３
(イ)より、４３

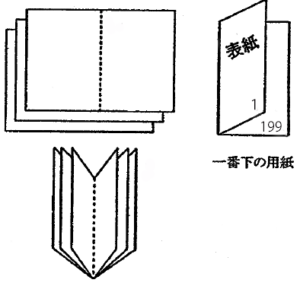
ページ番号の論理と推理（昭和学院秀英中学　2010年）

図のように紙を重ねて２つ折りにした２００ページの冊子があります。
６３ページを含む用紙で、６３以外のページ番号を、小さい順に答えてください。
10161

○ 正解
「チャレペ～」に同じような問題がありました。一度、経験済みなので解けた感じ。左上の図にある紙3枚分だけでも、ページ数を入れていってみると、すぐに規則性に気づきます。

（答）64、137、138ページ

どちらに何ｍ離れているか？（青山学院中等部　2013年）

東西にのびた道にＡ，Ｂ，Ｃ，Ｄ，Ｅの５つの地点があります。
Ａの東８０ｍにＢがあり、Ｃの西４０ｍにＤがあります。
ＤとＥは１１０ｍ、ＣとＢは１３０ｍ離れていて、
ＢはＥのとなりに、ＣはＡとＤの間にあります。
ＣとＥのまん中の地点は、
Ａから見てどちらの方角へ何ｍのところにありますか。

○ 正解
ややこしそうに見えて、実はそうでもない問題。条件を一個一個ちゃんと見て、可能性を潰していけばピースがハマっていきます。

Ｄ

40m

Ｃ

50m

Ａ

20m

Ｅ

60m

Ｂ

（答）西へ15m

４人の順位は？（東京都市大学等々力中学　2014年）

Ａ君、Ｂ君、Ｃ君、Ｄ君の４人が５０ｍ走をし、
その結果について次のように述べています。
Ａ君「僕は３位の人より２秒早くゴールした｡」
Ｂ君「僕は秒速５ｍの速さで走った｡」
Ｃ君「僕の記録は１２．５秒だった｡」　
Ｄ君「僕は４位の人の２倍の速さで走った｡」
このとき、４人の順位はどうなっていましたか。
また、２位の人の速さは毎秒何ｍですか。

○ 正解

		速さ	タイム
1位	Ｄ	8m/秒	6.25秒
2位	Ａ	6.25m/秒	8秒
3位	Ｂ	5m/秒	10秒
4位	Ｃ	4m/秒	12.5秒

鍵が外れる数字は？（2015年　東海大学付属浦安高等学校中等部）

４つの数字をあわせるダイヤル式の鍵があります。
それぞれのダイヤルには０～９の数字が書かれています。
図１は，ダイヤルが８３０１となっています。
414

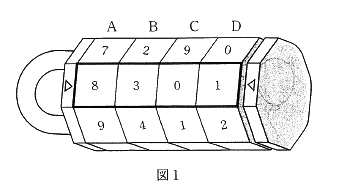
Ａ～Ｄの数が，次の条件①～⑤をすべてみたすと，鍵がはずれます。
①ＡとＢとＣとＤの和は１２です。
②ＡとＢとＣの和はＤに等しくなります。
③ＡとＢの積はＣとＤの積と等しくなります。
④図１の状態で，すでに１つの数字はあっています。
⑤ＡとＢとＣとＤはすべて異なります。
①～⑤より，鍵がはずれた時の４つの数字はいくつですか。

○ 正解
これはもはや代入法にほかならない。
A+B+C+D=12
A+B+C=D
したがって、D=6
A,B,C は１,２,３のどれかに絞られたが、次の条件 A×B=C×D はそのまま使うのではなく、A:C=D:B と姿を変えて解けるとうれしい。
A=2 , B=3 , C=1 , D=6

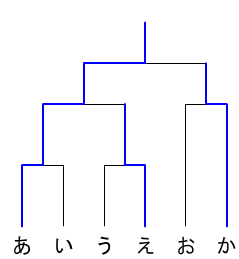
トーナメントの勝敗は？（2015年　早稲田中学）

図のトーナメント表はA～Fのチームの勝敗が記録されています。
勝ち進んだ場合は太線（青）になっています。
各チームは結果について次のように言っています。
　Ａ：１試合目で負けてしまったが、もし勝ち進んでいたら３試合勝てば優勝できた。
　Ｂ：Ａとは戦わなかった。
　Ｃ：Ｄと戦って負けてしまった。
　Ｄ：２試合目にＢと戦った。
　Ｅ：Ｃとは戦わなかった。
　Ｆ：１試合目は勝った。
このとき、トーナメント表の(い)と(か)に入るチームをそれぞれ答えなさい。
3271

○ 正解

あ	い	う	え	お	か
Ｂ	Ｅ	Ａ	Ｆ	Ｃ	Ｄ

伝説の名作問題（武蔵中学　２００５年）

生徒40人のクラスで希望者に花の種を，みな同数になるように配ることにしました。はじめ，希望者に配ったところ種は全部なくなりました。ところが，あとで希望者が3人増えたので配り直したところ，種は18粒余り，あと1粒ずつは配れませんでした。このとき先生は，「あと3人分はないけれども2人分はあるぞ」と言いました。はじめの希望者は何人だったでしょうか。

× 不正解
これは難問！解けなくてもしょうがないな。受験生なら解けてほしいけど。

（答）21人

参照：どう解く？中学受験算数より

とっかかりが見つからないときは